深度学习Q-learing算法实现
1. 问题分析
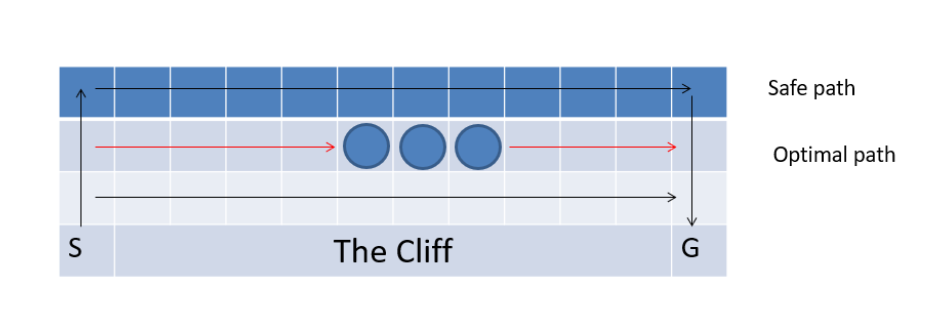
这是一个走悬崖的问题。强化学习中的主体从S出发走到G处一个回合结束,除了在边缘以外都有上下左右四个行动,如果主体走入悬崖区域,回报为-100,走入中间三个圆圈中的任一个,会得到-1的奖励,走入其他所有的位置,回报都为-5。
这是一个经典的Q-learing问题走悬崖的问题,也就是让我们选择的最大利益的路径,可以将图片转化为reward矩阵
1
2
3
4
| [[ -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5.]
[ -5. -5. -5. -5. -5. -1. -1. -1. -5. -5. -5. -5.]
[ -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5. -5.]
[ -5. -100. -100. -100. -100. -100. -100. -100. -100. -100. -100. 100.]]
|
我们的目标就是让agent从s(3,0)到达g(3,11)寻找之间利益最大化的路径,学习最优的策略。
2. Q—learing理论分析
在Q-learing算法中有两个特别重要的术语:状态(state),行为(action),在我们这个题目中,state对应的就是我们的agent在悬崖地图中所处的位置,action也就是agent下一步的活动,我的设定是(0, 1 ,2,3,4)对应的为(原地不动,上,下,左,右),需要注意的事我们的next action是随机的但是也是取决于目前的状态(current state)。
我们的核心为Q-learing的转移规则(transition rule),我们依靠这个规则去不断地学习,并把agent学习的经验都储存在Q-stable,并不断迭代去不断地积累经验,最后到达我们设定的目标,这样一个不断试错,学习的过程,最后到达目标的过程为一个episode
$$Q(s,a) = R(s,a)+\gamma *max \lbrace Q(\tilde{s},\tilde{a}) \rbrace $$
其中$s,a$表示现在状态的state和action,$\tilde{s},\tilde{a}$表示下一个状态的state和action,学习参数为$0<\gamma<1$,越接近1代表约考虑远期结果。
在Q-table初始化时由于agent对于周围的环境一无所知,所以初始化为零矩阵。
3. 算法实现
参考以下伪代码:

具体程序如见附录
程序的关键点:
- 核心代码即为伪代码,但是各种方法需要自己实现,在程序中有注释可以参考
- 需要判断agent在一个状态下可以使用的行动,这一点我用
valid_action(self, current_state)实现
发现的问题:题目中的目标点为G 的目标值也是为-1,但是程序会走到这个一步但是函数没有收敛到此处,而且由于在奖励点收益大,所以最后的agent会收敛到奖励点处,在三个奖励点处来回移动。所有我将最后的目标点G的值改为了100,函数可以收敛到此处。后来也看到文献中的吸收目标
3. 结果展示
最后到Q-tabel矩阵由于太大放到附录查看,但是同时为了更加直观的看到运行结果,
编写了动态绘图的程序 画出了所有的路径。如果需要查看动态图片请运行程序最终结果如下图:
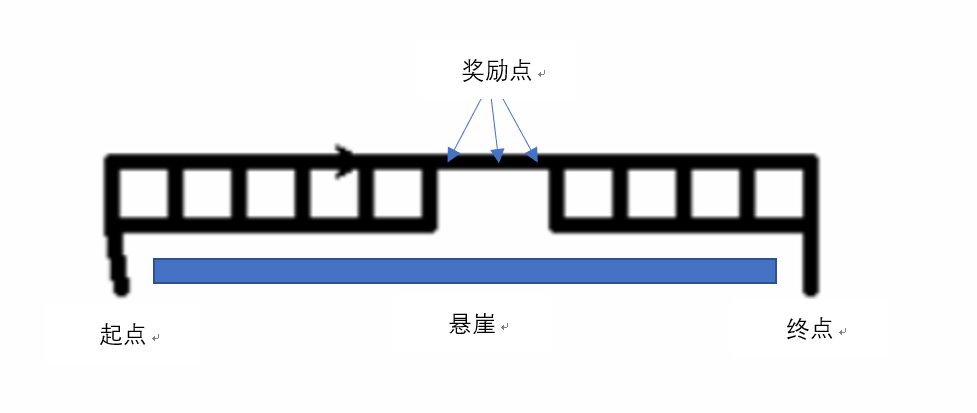
从图中可以看到agent避过了所有的悬崖,而且收获了所有的奖励最终到达目标。
4.附录
程序:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
|
import numpy as np
import random
import turtle as t
class Cliff(object):
def __init__(self):
self.reward = self._reward_init()
print(self.reward)
self.row = 4
self.col = 12
self.gamma = 0.7
self.start_state = (3, 0)
self.end_state = (3, 11)
self.q_matrix = np.zeros((4,12,5))
self.main()
def _reward_init(self):
re = np.ones((4,12))*-5
re[1][5:8] = np.ones((3))*-1
re[3][1:11] = np.ones((10))*-100
re[3][11] = 100
return re
def valid_action(self, current_state):
itemrow, itemcol = current_state
valid = [0]
if(itemrow-1 >= 0): valid.append(1)
if(itemrow+1 <= self.row-1):valid.append(2)
if(itemcol-1 >= 0): valid.append(3)
if(itemcol+1 <= self.col-1): valid.append(4)
return valid
def transition(self, current_state, action):
itemrow, itemcol = current_state
if (action is 0): next_state = current_state
if (action is 1): next_state = (itemrow-1, itemcol)
if (action is 2): next_state = (itemrow+1, itemcol)
if (action is 3): next_state = (itemrow, itemcol-1)
if (action is 4): next_state = (itemrow, itemcol+1)
return(next_state)
def _indextoPosition(self,index):
index += 1
itemrow = int(np.floor(index/self.col))
itemcol = index%self.col
return(itemrow, itemcol)
def _positiontoIndex(self,itemrow,itemcol):
itemindex = (itemrow)*self.col+itemcol-1
return itemindex
def getreward(self, current_state, action):
next_state = self.transition(current_state, action)
next_row, next_col = next_state
r = self.reward[next_row, next_col]
return r
def path(self):
t.speed(10)
t.begin_fill()
paths = []
current_state = self.start_state
t.pensize(5)
t.penup()
t.goto(current_state)
t.pendown()
paths.append(current_state)
while current_state != self.end_state:
current_row, current_col = current_state
valid_action = self.valid_action(current_state)
valid_value = [self.q_matrix[current_row][current_col][x] for x in valid_action]
max_value = max(valid_value)
action = np.where(self.q_matrix[current_row][current_col] == max_value)
print(current_state,'-------------',action)
next_state = self.transition(current_state,int(random.choice(action[0])))
paths.append(next_state)
next_row,next_col = next_state
t.goto(next_col*20, 60-next_row*20)
current_state = next_state
def main(self):
for i in range(1000):
current_state = self.start_state
while current_state != self.end_state:
action = random.choice(self.valid_action(current_state))
next_state = self.transition(current_state, action)
future_rewards = []
for action_next in self.valid_action(next_state):
next_row, next_col = next_state
future_rewards.append(self.q_matrix[next_row][next_col][action_next])
q_state = self.getreward(current_state, action) + self.gamma*max(future_rewards)
current_row, current_col = current_state
self.q_matrix[current_row][current_col][action] = q_state
current_state = next_state
for i in range(1000):
self.path()
print(self.q_matrix)
if __name__ == "__main__":
Cliff()
|
Q-table矩阵最终结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| [[[ -14.84480118 0. -14.06400168 0. -14.06400168]
[ -14.06400168 0. -12.94857383 -14.84480118 -12.94857383]
[ -12.94857383 0. -11.35510547 -14.06400168 -11.35510547]
[ -11.35510547 0. -9.07872209 -12.94857383 -9.07872209]
[ -9.07872209 0. -5.82674585 -11.35510547 -5.82674585]
[ -5.82674585 0. -1.1810655 -9.07872209 -5.1810655 ]
[ -5.1810655 0. -0.258665 -5.82674585 -4.258665 ]
[ -4.258665 0. 1.05905 -5.1810655 -2.94095 ]
[ -2.94095 0. 2.9415 -4.258665 2.9415 ]
[ 2.9415 0. 11.345 -2.94095 11.345 ]
[ 11.345 0. 23.35 2.9415 23.35 ]
[ 23.35 0. 40.5 11.345 0. ]]
[[ -14.06400168 -14.84480118 -14.84480118 0. -12.94857383]
[ -12.94857383 -14.06400168 -14.06400168 -14.06400168 -11.35510547]
[ -11.35510547 -12.94857383 -12.94857383 -12.94857383 -9.07872209]
[ -9.07872209 -11.35510547 -11.35510547 -11.35510547 -5.82674585]
[ -5.82674585 -9.07872209 -9.07872209 -9.07872209 -1.1810655 ]
[ -1.1810655 -5.82674585 -5.82674585 -5.82674585 -0.258665 ]
[ -0.258665 -5.1810655 -2.94095 -1.1810655 1.05905 ]
[ 1.05905 -4.258665 2.9415 -0.258665 2.9415 ]
[ 2.9415 -2.94095 11.345 1.05905 11.345 ]
[ 11.345 2.9415 23.35 2.9415 23.35 ]
[ 23.35 11.345 40.5 11.345 40.5 ]
[ 40.5 23.35 65. 23.35 0. ]]
[[ -14.84480118 -14.06400168 -15.39136082 0. -14.06400168]
[ -14.06400168 -12.94857383 -109.84480118 -14.84480118 -12.94857383]
[ -12.94857383 -11.35510547 -109.06400168 -14.06400168 -11.35510547]
[ -11.35510547 -9.07872209 -107.94857383 -12.94857383 -9.07872209]
[ -9.07872209 -5.82674585 -106.35510547 -11.35510547 -5.82674585]
[ -5.82674585 -1.1810655 -104.0787221 -9.07872209 -2.94095 ]
[ -2.94095 -0.258665 -102.058665 -5.82674585 2.9415 ]
[ 2.9415 1.05905 -97.94095 -2.94095 11.345 ]
[ 11.345 2.9415 -92.0585 2.9415 23.35 ]
[ 23.35 11.345 -83.655 11.345 40.5 ]
[ 40.5 23.35 -30. 23.35 65. ]
[ 65. 40.5 100. 40.5 0. ]]
[[ -15.39136082 -14.84480118 0. 0. -109.84480118]
[-109.84480118 -14.06400168 0. -15.39136082 -109.06400168]
[-109.06400168 -12.94857383 0. -109.84480118 -107.94857383]
[-107.94857383 -11.35510547 0. -109.06400168 -106.35510547]
[-106.35510547 -9.07872209 0. -107.94857383 -104.0787221 ]
[-104.0787221 -5.82674585 0. -106.35510547 -102.058665 ]
[-102.058665 -2.94095 0. -104.0787221 -97.94095 ]
[ -97.94095 2.9415 0. -102.058665 -92.0585 ]
[ -92.0585 11.345 0. -97.94095 -83.655 ]
[ -83.655 23.35 0. -92.0585 -30. ]
[ -30. 40.5 0. -83.655 100. ]
[ 0. 0. 0. 0. 0. ]]]
|


